数学函数是数学学科的重要组成部分，其在各个领域的应用十分广泛，为了更好地理解和掌握数学函数，本文将针对数学函数进行专题归纳，梳理其基本概念、性质以及常见类型，以便读者更好地理解和掌握。

数学函数的基本概念

1、函数的定义

函数是一种数学关系，表示输入值与输出值之间的对应关系，在函数中，每个输入值（自变量）对应一个唯一的输出值（因变量）。

2、函数的表示方法

函数可以通过多种方式表示，如解析法、表格法、图示法等，解析法是最常用的方法，通过数学表达式来描述自变量与因变量之间的关系。

数学函数的性质

1、函数的定义域与值域

函数的定义域是指自变量可以取值的范围，值域是指因变量可以取值的范围，了解函数的定义域和值域对于理解函数的性质和应用至关重要。

2、函数的单调性

函数在某个区间内的单调性取决于其导数在该区间内的符号，导数大于零时，函数单调递增；导数小于零时，函数单调递减。

3、函数的奇偶性

奇函数是关于原点对称的函数，即对于所有x，都有f(-x)=-f(x)；偶函数是关于y轴对称的函数，即对于所有x，都有f(-x)=f(x)，了解函数的奇偶性有助于简化函数的求解过程。

常见数学函数类型及其性质

1、线性函数

线性函数是最简单的函数类型之一，其图像为一条直线，线性函数具有固定斜率，且满足f(x)=kx+b（k为斜率，b为截距）。

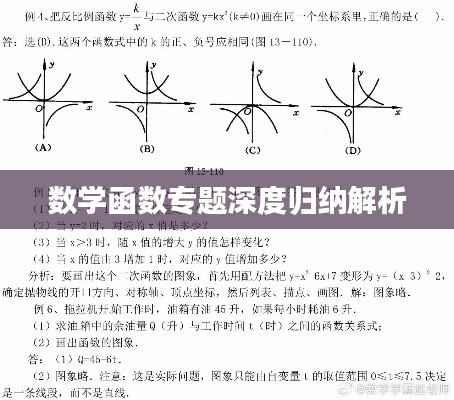
2、二次函数

二次函数是一种多项式函数，其一般形式为f(x)=ax²+bx+c（a≠0），二次函数的图像为抛物线，其顶点、对称轴和与坐标轴的交点等性质对于解决实际问题具有重要意义。

3、三角函数

三角函数包括正弦函数、余弦函数、正切函数等，这些函数在几何、物理、工程等领域有广泛应用，三角函数的周期性、奇偶性、单调性等性质对于理解和应用三角函数至关重要。

4、指数函数与对数函数

指数函数具有形式f(x)=ax（a>0，a≠1），对数函数是指数函数的反函数，这两种函数在金融学、统计学、生物学等领域有广泛应用，指数函数具有增长迅速的性质，而对数函数则具有将乘法转换为加法的特点。

本文对数学函数进行了专题归纳，梳理了数学函数的基本概念、性质以及常见类型，掌握数学函数的基本概念和性质，对于理解和应用数学函数具有重要意义，在实际问题中，根据具体情况选择合适的函数类型进行建模，可以简化问题求解过程，希望本文能对读者在数学函数的学习和应用上有所帮助。